本节课是通过任务实例展开的,首先介绍了Word Window Classification任务,之后用softmax和cross-entropy进行线性分类,之后用神经网络进行了非线性分类(引入Max-Margin loss & back propogation),其间对相关方法进行了讲解。
Simple word classfication task —— linear classfication
- 输入输出: \(\{x_i, y_i\}^N_{i=1}\)
\(x_i\): 词向量
\(y_i\): 输出的分类结果(各个类别的概率分布) - 分类公式:
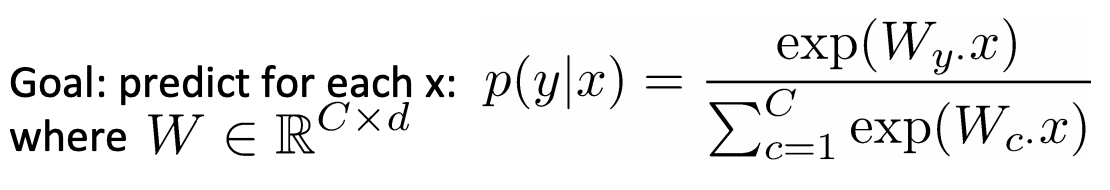
注:分类逻辑就相当于蕴含在矩阵\(W\)中 - Loss function:
但光有分类公式还不够,我们还要使分类结果最优,即:使整个数据集的分类结果\(P(y|x)\)最优(一个\(P(y|x)\)只是针对单个词的分类结果),因此就有了损失函数。 - 交叉熵:其中涉及到了Kullback-Leibler divergence(KL散度),其可用于衡量两个概率之间的误差,在这个任务中我们可以用来衡量\(P(y|x)\)和ground truth/gold/target probability(即正确的分类结果:[0,…0,1,0,…0],一个为1,其余为0)的误差。误差越小,代表分类结果越好。
- 交叉熵公式:$$H(p, q) = -\sum_{c=1}^Cp(c)logq(c)$$
我们把p(c)看成gold,把q(c)看成预测结果,就有了我们最后的损失函数。 - 损失函数:
$$
J(\theta) = \frac {1} {N} \sum_{i=1}^N -log(\frac {exp(f_{yi})} {\sum_{c=1}^Cexp(f_c)})
$$
注1: \(f = Wx\)
注2: 最终最小化损失函数即可(Maxmize \(P(y|x)\) -> Minimize \(-logP(y|x)\))。分类问题中是否更新词向量
- 在优化损失函数的时候,可以只选择\(W\)作为优化参数, 但可将词向量作为一个参数也同时进行梯度下降更新,从而使得词向量更为适合当前任务。
- 判断标准:当前任务的数据集的大小。若当前任务数据集不大,则更新词向量很有可能会contaminate原先的向量空间,使得效果反而下降;但若数据集总量很大,可以保证词向量优化效果,且计算资源充足,则应进行优化。
Word Window Classification
- 任务目标: Classify a word in its context window of neighboring words.
eg. 命名实体识别任务: 对单词是Person, location, organization还是none进行分类。 - 相比于单个单词的分类,Word Window Classification是将上下文单词也进行考虑,从而帮助对中心词的分类。
- 与上文的单词分类相比,唯一改变的只是输入\(x_i\),原来是一个单词的词向量,现在输入的是整个window所有单词词向量的拼接(concatenation)。通过整个window的context words来帮助对中心词的分类。
- 注:window模型有很多种处理方式,如可以将window中的所有单词不考虑位置作乱序处理,以及其他方法来更多地探索上下文信息。
神经网络分类
- 只用SoftMax分类的问题:只能提供线性分类的结果,在复杂数据集上的表现不好。
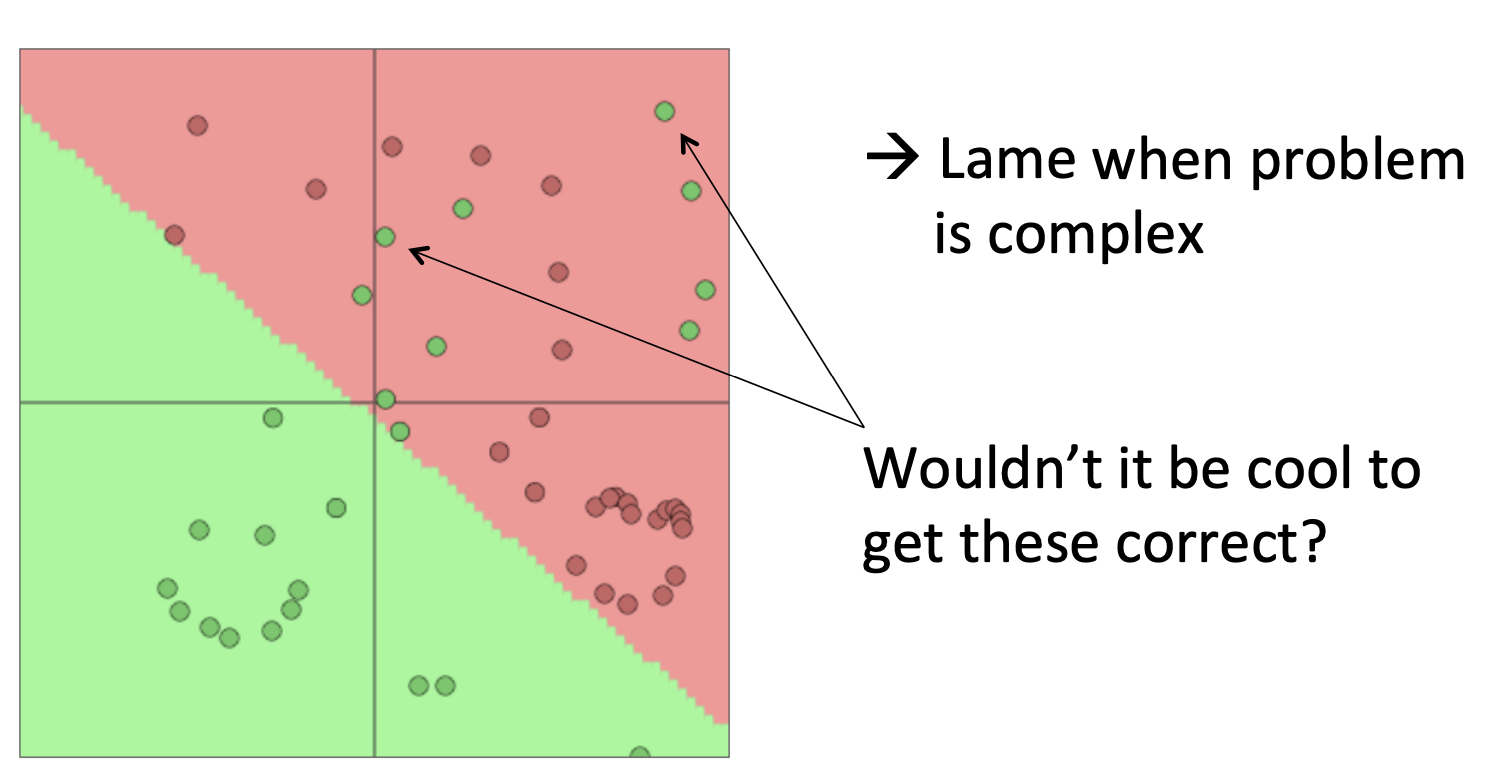
- 神经网络的优点是具有强大的非线性拟合能力,而这种拟合能力很大程度上来源于神经元各种各样的非线性激活函数。
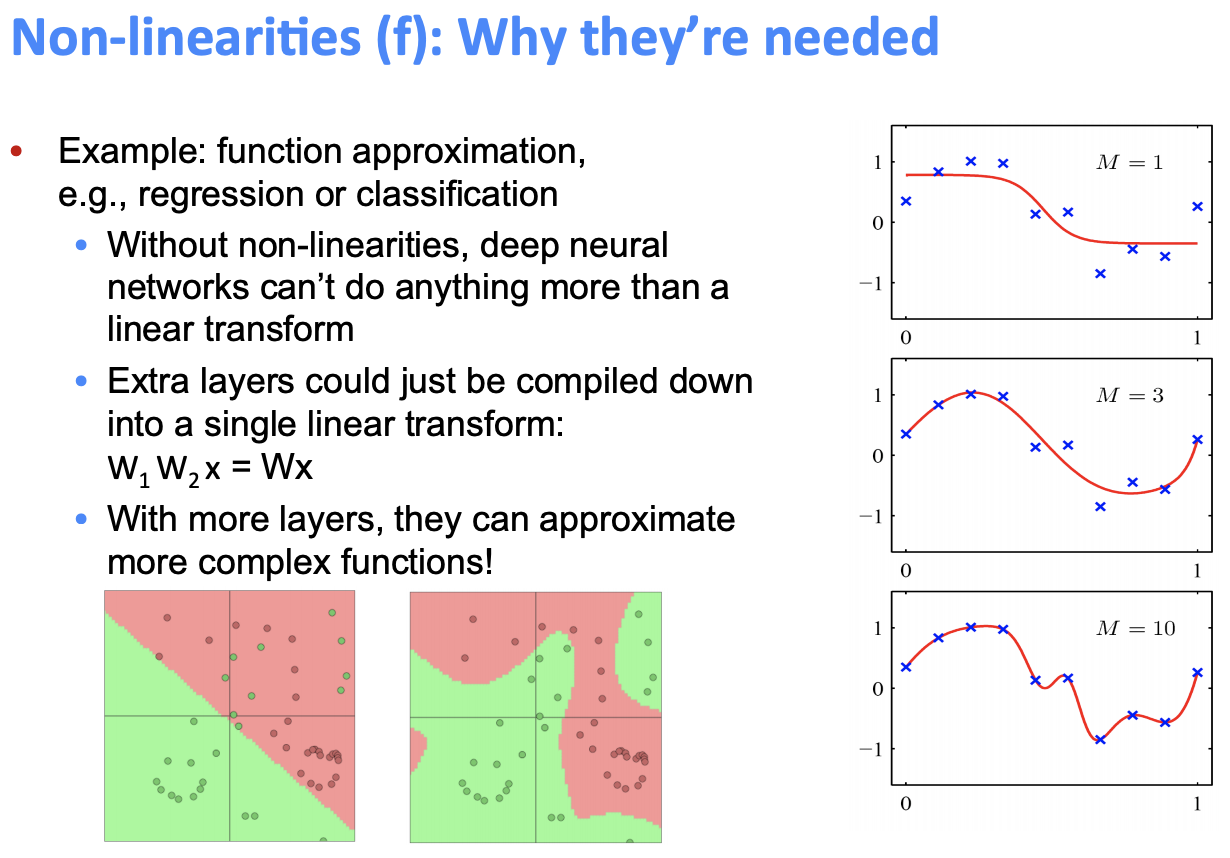
- Max-margin Loss function
依旧是ner的任务,对单词是不是地点进行分类。
s = score(museums in Paris are amzing):中心词是地点的句子
sc = score(Not all meseums in Paris):中心词不是地点的句子
公式:$$ J = max(0, 1-s+sc) $$
idea:将中心词是地点的句子(正例)的得分最大化,中心词不是地点的句子(负例)的得分最小化。即正例句子的分值要比负例句子的分值 > 1。
注1:将\(J\)值最小化即可 -> 0。
注2:公式中的1可看作一个超参数,通常是1,也可是其他数。
注3:公式是连续的,因此可使用SGD。
Post Date: 2019-01-27
版权声明: 本文为原创文章,转载请注明出处